n-Local Chain Inequality¶
The \(n\)-local chain network consists of \(n\) entanglement sources (static preparation node) and \(n+1\) measurement nodes linked as a chain by the entanglement sources.
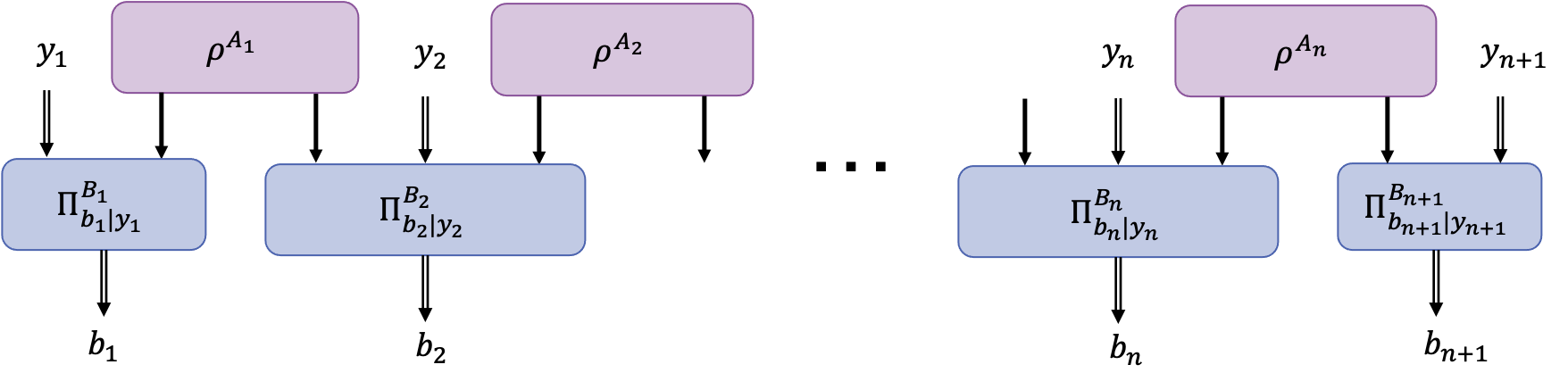
\(n\) -Local Chain Network.¶
If the entanglement sources are compared directly to classical shared randomness, then polynomial Bell inequalities can be derivied that tightly bound the set of classical correlations [Branciard2012], [Mukherjee2015]. These \(n\) -local Bell inequalities can witness quantum violations to the classical \(n\) -local set. The variations of these inequalities and their quantum violations are discussed further as they are integrated into cost functions.
- qnetvo.nlocal_chain_22_cost_fn(network_ansatz, parallel=False, **qnode_kwargs)[source]¶
For the provided
network_ansatz, constructs the cost function for the \(n\)-local chain Bell inequality for binary inputs and outputs.- Parameters:
network_ansatz (qnet.NetworkAnsatz) – The ansatz for the networks.
parallel (optional bool) – If
True, remote qnode executions are made in parallel web requests.
\[Cost(\vec{\theta}) = - \left(\sqrt{|I_{22}^n|} + \sqrt{|J_{22}^n|} \right)/2\]where the quantities \(I_{22}^n\) and \(J_{22}^n\) are defined as
\[\begin{split}I_{22}^n &:= \frac{1}{4} \sum_{y_1,y_{n+1}=0}^{1}\langle B^1_{y_1}B^2_0\dots B^{n}_0B^{n+1}_{y_{n+1}}\rangle_{22}, \\ J_{22}^n &:= \frac{1}{4} \sum_{y_1,y_{n+1}=0}^{1}(-1)^{y_1+y_{n+1}}\langle B_{y_1}^{B_{1}^2}\dots B_{1}^{n}B_{y_{n+1}}^{n+1} \rangle_{22},x\end{split}\]and the \(n\)-local correlator is defined as
\[\langle B^1_{y_1}\dots B^{n+1}_{y_{n+1}} \rangle_{22} = \text{Tr}\left[\left( \bigotimes_{j=1}^{n+1} B^j_{y_j}\right) \bigotimes_{i=1}^n \rho^{A^iA^{i+1}} \right],\]with \(B^j_{y_j}\) being a dichotomic parity observable at the \(j^{th}\) measurement node. Note that the \(n\)-local correlator is simply a parity measurement distributed across all measurement nodes in the network.
The maximal score for the dichotomic \(n\) -local Bell inequality is known to be \(\sqrt{2} \approx 1.414 213\).
- Returns:
A cost function that can be evaluated as
cost(*network_settings)wherenetwork_settingshave the appropriate dimensions for the providednetwork_ansatz- Return type:
Function
- qnetvo.chain_I22_fn(network_ansatz, parallel=False, **qnode_kwargs)[source]¶
Constructs a function for evaluating the \(I_{22}\) quantity used in the
nlocal_chain_22_cost_fnfunction.- Parameters:
network_ansatz (qnet.NetworkAnsatz) – The ansatz for the \(n\)-local chain network.
parallel (optional bool, default
False) – IfTrue, remote qnode executions are made in parallel web requests.qnode_kwargs – keyword args to be passed to constructed QNodes.
- Type:
optional dictionary
- Returns:
A function callable as
I22(*network_settings)that evaluates the \(I_{22}\) quantity.- Return type:
function
- qnetvo.chain_J22_fn(network_ansatz, parallel=False, **qnode_kwargs)[source]¶
Constructs a function for evaluating the \(J_{22}\) quantity used in the
nlocal_chain_22_cost_fnfunction.- Parameters:
network_ansatz (qnet.NetworkAnsatz) – The ansatz for the \(n\)-local chain network.
parallel (optional bool, default
False) – IfTrue, remote qnode executions are made in parallel web requests.qnode_kwargs – keyword args to be passed to constructed QNodes.
- Type:
optional dictionary
- Returns:
A function callable as
J22(*network_settings)that evaluates the \(J_{22}\) quantity.- Return type:
function
- qnetvo.parallel_nlocal_chain_grad_fn(network_ansatz, natural_grad=False, **qnode_kwargs)[source]¶
Constructs a parallelizeable gradient function
grad_fnfor the \(n\)-local chain cost.The parallelization is achieved through multithreading and intended to improve the efficiency of remote qnode execution. The number of threads is restricted to four in order to be compatible with IBM’s API.
- Parameters:
network_ansatz (NetworkAnsatz) – The ansatz describing the \(n\)-local chain network.
natural_grad (optional Bool) – If
True, the natural gradient is evaluated by scaling the gradient by the inverse of the metric tensor.qnode_kwargs (optional dict) – A keyword argument passthrough to qnode construction.
- Returns:
A parallelized (multithreaded) gradient function
nlocal_chain_grad(*network_settings).- Return type:
function
Warning
Parallel gradient computation is flaky on PennyLane v0.28+. Intermittent failures may occur.
References¶
Branciard, Cyril, et al. “Bilocal versus nonbilocal correlations in entanglement-swapping experiments.” Physical Review A 85.3 (2012): 032119.
Mukherjee, Kaushiki, Biswajit Paul, and Debasis Sarkar. “Correlations in \(n\) -local scenario.” Quantum Information Processing 14.6 (2015): 2025-2042.