A Test for Classical Dimension

In this device-indepenendent test, Alice encodes $x\in\{0,1,2,3\}$ into the states $\{|00\rangle, |01\rangle, |10\rangle, |11\rangle\}$. Bob measures in the computational basis and outputs the result, $b\in \{0,1,2,3\}$.

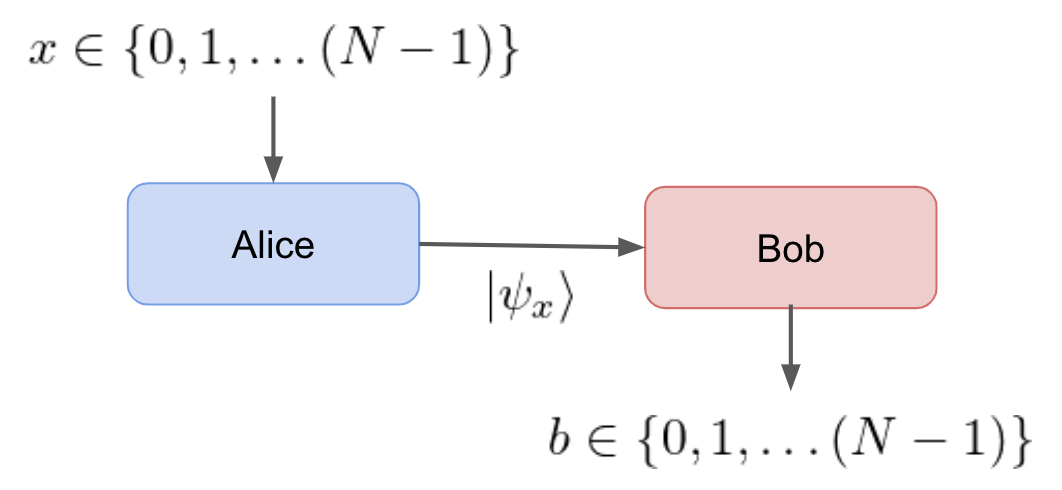
The success probability for quantum and classical scenarios is bounded by

$$\frac{d}{N} \geq \frac{1}{N}\sum_{x=0}^{N-1} p(b=x,x),$$

where $d$ is the number of dimensions in the hilbert space and $N$ is the number of inputs $x$. Classical systems perform as well as quantum systems for this "guessing game" task. The objective is not to determine quantum or classical in this test, but to verify the ability to send a $d$ dimensional qubit state by using all of the orthogonal axes to encode classical information. This test could also be effective at measuring the noise in a quantum channel.

We now demonstrate an implementation of this test to verify the ability to send to qubits in the computational basis.

from qiskit import QuantumCircuit,execute, IBMQ
from qiskit.tools.monitor import *
from qiskit.providers.ibmq.managed import IBMQJobManager

provider = IBMQ.load_account()

import matplotlib.pyplot as plt
import numpy as np

import context
from device_independent_test import dimension
from device_independent_test.handshake import HandShake
from device_independent_test.quantum_communicator import LocalDispatcher

ibmqfactory.load_account:WARNING:2020-07-01 12:36:02,636: Credentials are already in use. The existing account in the session will be replaced.

Running a Dimensionality Test Through HandShake

The implemented circuit is an identity circuit. This test is testing the noise of a quantum channel.

Qiskit Simulator

# load the dispatcher
dispatcher = LocalDispatcher([provider.get_backend('ibmq_qasm_simulator')])
handshake = HandShake(dispatcher)

# set the tolerance and shots
tolerance = 0.1
shots = 1000

# run the dimensionality test
handshake.dimensionality(tolerance, shots)

Passed Dimensionality with value:  1.0





(True, 1.0)

IBM Quantum Machine

dispatcher = LocalDispatcher([provider.get_backend('ibmq_london')])
handshake = HandShake(dispatcher)

tolerance = 0.1
shots = 1000
handshake.dimensionality(tolerance, shots)

Passed Dimensionality with value:  0.9145





(True, 0.9145)

The IBM quantum machine is expected to perform worse than the simulator due to noise, even in this case where very few operations are performed.

Implementation Details: Alice and Bob verify the ability to send two bits.

Alice and Bob can prepare and measure a set of orthogonal measurements on a 4-dimensional Hilbert space. Alice simply encodes the input $x\in\{0,1,2,3\}$ into the bit string and Bob decodes it without error. Assuming a uniform prior distribution for $x$, the success probability for this case is $1 \geq 1/4 \sum_x p(b=x|x)$.

Prepare and Measure Qubit States

# alice prepares the complete set of orthogonal states

qc_00 = dimension.prepare_bit_circuit([0,0])
qc_01 = dimension.prepare_bit_circuit([0,1])
qc_10 = dimension.prepare_bit_circuit([1,0])
qc_11 = dimension.prepare_bit_circuit([1,1])

circuits = [qc_00, qc_01, qc_10, qc_11]

# Bob measures in the computational basis.
for qc in circuits:
    qc.measure_all()

for qc in circuits:
    display(qc.draw())

         ░ ┌─┐   
   q_0: ─░─┤M├───
         ░ └╥┘┌─┐
   q_1: ─░──╫─┤M├
         ░  ║ └╥┘
meas_0: ════╩══╬═
               ║ 
meas_1: ═══════╩═
                 

              ░ ┌─┐   
   q_0: ──────░─┤M├───
        ┌───┐ ░ └╥┘┌─┐
   q_1: ┤ X ├─░──╫─┤M├
        └───┘ ░  ║ └╥┘
meas_0: ═════════╩══╬═
                    ║ 
meas_1: ════════════╩═
                      

        ┌───┐ ░ ┌─┐   
   q_0: ┤ X ├─░─┤M├───
        └───┘ ░ └╥┘┌─┐
   q_1: ──────░──╫─┤M├
              ░  ║ └╥┘
meas_0: ═════════╩══╬═
                    ║ 
meas_1: ════════════╩═
                      

        ┌───┐ ░ ┌─┐   
   q_0: ┤ X ├─░─┤M├───
        ├───┤ ░ └╥┘┌─┐
   q_1: ┤ X ├─░──╫─┤M├
        └───┘ ░  ║ └╥┘
meas_0: ═════════╩══╬═
                    ║ 
meas_1: ════════════╩═
                      

The displayed circuits show the gates that are being run in our simulation.

Run on the Qiskit Simulator

# running tests on quantum computer

def run_job(qc, shots):
    job = execute(qc, backend=provider.get_backend('ibmq_qasm_simulator'), shots=shots)
    job_monitor(job)
    return job

shots = 1000
d4_job_00 = run_job(qc_00, shots)
d4_job_01 = run_job(qc_01, shots)
d4_job_10 = run_job(qc_10, shots)
d4_job_11 = run_job(qc_11, shots)

Job Status: job has successfully run
Job Status: job has successfully run
Job Status: job has successfully run
Job Status: job has successfully run

Compute the Success Probability of the Measurements

The optimal score is 1.0 for a scenario where two bits or qubits are used.

# parsing statistics
d4_counts_00 = d4_job_00.result().get_counts()
d4_counts_01 = d4_job_01.result().get_counts()
d4_counts_10 = d4_job_10.result().get_counts()
d4_counts_11 = d4_job_11.result().get_counts()

# success probability for a d=4 system is 1
p_succ_00 = d4_counts_00["00"]/shots
p_succ_01 = d4_counts_01["10"]/shots # qiskits labeling is weird
p_succ_10 = d4_counts_10["01"]/shots # qiskits labeling is weird
p_succ_11 = d4_counts_11["11"]/shots

d4_success_probability = (p_succ_00 + p_succ_01 + p_succ_10 + p_succ_11)/4 # divide by 4 because there are 4 inputs.

d4_success_probability

1.0

Test Failure: Alice only has access to 1-qubit

In this scenario, Alice can only send 1-qubit, the second register is constant. The encoded qubits are $\{|00\rangle, |00\rangle, |10\rangle |11\rangle \}$. The measurement success_probability is therefor $0.5 \geq 1/4 \sum_x p(b=x|x)$.

Running jobs

shots = 1000
d2_job_00 = run_job(qc_00, shots)
d2_job_01 = run_job(qc_00, shots)
d2_job_10 = run_job(qc_10, shots)
d2_job_11 = run_job(qc_10, shots)

Job Status: job has successfully run
Job Status: job has successfully run
Job Status: job has successfully run
Job Status: job has successfully run

Calculating Success Probability

counts_00 = d2_job_00.result().get_counts()
counts_01 = d2_job_01.result().get_counts()
counts_10 = d2_job_10.result().get_counts()
counts_11 = d2_job_11.result().get_counts()

d2_p_succ_00 = counts_00["00"]/shots if ("00" in counts_00) else 0.0
d2_p_succ_01 = counts_01["10"]/shots if ("10" in counts_01) else 0.0 # qiskits labeling is weird
d2_p_succ_10 = counts_10["01"]/shots if "01" in counts_10 else 0.0 # qiskits labeling is weird
d2_p_succ_11 = counts_11["11"]/shots if "11" in counts_11 else 0.0

d2_success_probability = (d2_p_succ_00 + d2_p_succ_01 + d2_p_succ_10 + d2_p_succ_11)/4

d2_success_probability # the classical bound is 0.5 

0.5

The test fails because the bound of 1.0 is not reached. The maximal score for the single qubit is 0.5.